Câu hỏi:
26/04/2022 136,663
Đáp án chủ yếu xác
Ta có: \(\mathop {\lim }\limits_{x \to \pm \infty } hắn = 2 \Rightarrow \) đường thẳng liền mạch \(y = 2\)là tiệm cận ngang của thiết bị thị hàm số.
\(\mathop {\lim }\limits_{x \to {3^ + }} hắn = + \infty ;\mathop {\lim }\limits_{x \to {3^ - }} hắn = - \infty \Rightarrow \) đường thẳng liền mạch \(x = 3\) là tiệm cận đứng của thiết bị thị hàm số.
Vậy tâm đối xứng của thiết bị thị là \(A\left( {3;2} \right).\)
Đáp án A
Nhà sách VIETJACK:
🔥 Đề đua HOT:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tìm \(m\) nhằm hàm số \(y = \frac{1}{3}{x^3} - m{x^2} + \left( {{m^2} - 4} \right)x + 3\) đạt cực lớn bên trên điểm x=3.
Câu 2:
Có từng nào độ quý hiếm vẹn toàn của thông số \(m\) nằm trong đoạn \(\left[ { - 20;2} \right]\) nhằm hàm số đồng trở nên bên trên \(\mathbb{R}.\)
Câu 3:
Cho lăng trụ đứng \(ABC.A'B'C'\) có tính nhiều năm cạnh mặt mày là \(2a,\) lòng \(ABC\) là tam giác vuông cân nặng bên trên \(A,\) góc thân thích \(AC'\) và mặt mày phẳng lì \(\left( {BCC'B'} \right)\) vì như thế \({30^0}\) (tham khảo hình vẽ).
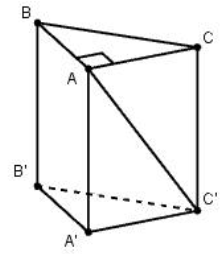
Tính bám theo \(a\) thể tích khối trụ với nhì lòng là hai tuyến đường tròn trĩnh nước ngoài tiếp nhì lòng của lăng trụ \(ABC.A'B'C'.\)
Câu 4:
Cho nhì số thực dương \(a,b.\) Rút gọn gàng biểu thức \[\] tớ chiếm được \(A = {a^m}.{b^n}.\)
Câu 5:
Viết phương trình tiếp tuyến của thiết bị thị hàm số \(y = \frac{{2x - 1}}{{x - 2}},\) biết tiếp tuyến với thông số góc \(k = - 3\)
Câu 6:
Cho hình lăng trụ đứng \(ABC.A'B'C'\) với lòng \(ABC\) vuông bên trên \(A,AB = a,BC = 2a,\) mặt mày mặt \(ACC'A'\) là hình vuông vắn. Gọi \(M,N,P\) theo thứ tự là trung điểm của \(AC,CC',A'B'\) và \(H\) là hình chiếu của \(A\) lên \(BC.\) Tính bám theo \(a\) khoảng cách thân thích hai tuyến đường trực tiếp \(MP\) và \(HN.\)
