I. Các kiến thức và kỹ năng cần thiết nhớ

Định nghĩa
Hai tam giác gọi là đồng dạng cùng nhau nếu như bọn chúng với tía cặp góc đều nhau từng song một và tía cặp cạnh ứng tỉ lệ thành phần.
Ví dụ: $\Delta ABC$ $\backsim$ $\Delta A'B'C'$\( \Leftrightarrow \left\{ \begin{array}{l}\widehat A = \widehat {A'},\,\widehat B = \widehat {B'},\widehat C = \widehat {C'}\\\dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{CA}}{{C'A'}}\end{array} \right.\)
Chú ý:
* Tỉ số những cạnh ứng \(\dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{CA}}{{C'A'}} = k\) được gọi là tỉ số đồng dạng của nhị tam giác.

Định lí về đưa đến nhị tam giác đồng dạng
Nếu một đường thẳng liền mạch hạn chế nhị cạnh của tam giác và tuy vậy song với cạnh sót lại thì nó tạo ra trở nên một tam giác mới mẻ đồng dạng với tam giác tiếp tục cho tới.

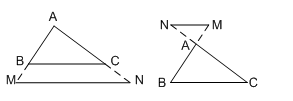
Cho $\Delta ABC$, $MN{\rm{//}}BC$
$ \Rightarrow \Delta AMN$$\backsim$$\Delta ABC.$
Chú ý: Định lí cũng giống nhập tình huống đường thẳng liền mạch hạn chế phần kéo dãn nhị cạnh của tam giác và tuy vậy song với cạnh sót lại.
II. Các dạng toán thông thường gặp
Dạng 1: Sử dụng tam giác đồng dạng nhằm tính phỏng nhiều năm cạnh, chu vi, tỉ số đồng dạng, số đo góc…
Phương pháp:
Ta dùng khái niệm và quyết định lý về nhị tam giác đồng dạng. Sử dụng quyết định lý Ta-lét và đặc điểm tỉ lệ thành phần thức nhằm đo lường.
$\Delta ABC$ $\backsim$ $\Delta A'B'C'$\( \Leftrightarrow \left\{ \begin{array}{l}\widehat A = \widehat {A'},\,\widehat B = \widehat {B'},\widehat C = \widehat {C'}\\\dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{CA}}{{C'A'}}\end{array} \right.\)
Dạng 2: Sử dụng tam giác đồng dạng nhằm chứng tỏ những nhân tố hình học tập (hai đường thẳng liền mạch tuy vậy tuy vậy, …)
Phương pháp:
Ta dùng $\Delta ABC$ $\backsim$ $\Delta A'B'C'$\( \Leftrightarrow \left\{ \begin{array}{l}\widehat A = \widehat {A'},\,\widehat B = \widehat {B'},\widehat C = \widehat {C'}\\\dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{CA}}{{C'A'}}\end{array} \right.\)
Và quyết định lý: Nếu một đường thẳng liền mạch hạn chế nhị cạnh của tam giác và tuy vậy song với cạnh sót lại thì nó tạo ra trở nên một tam giác mới mẻ đồng dạng với tam giác tiếp tục cho tới.
III. Bài luyện về tam giác đồng dạng
Câu 1: Cho tam giác $ABC$ đồng dạng với tam giác $A'B'C'$ . Hãy lựa chọn phát biểu sai:
A. \(\widehat A = \widehat {C'}\).
B. \(\dfrac{{A'B'}}{{AB}} = \dfrac{{A'C'}}{{AC}}\)
C. \(\dfrac{{A'B'}}{{AB}} = \dfrac{{B'C'}}{{BC}}\)
D. \(\widehat B = \widehat {B'}\)
Lời giải
\(\Delta ABC\) \(\backsim\) \(\Delta A'B'C'\) \( \Leftrightarrow \left\{ \begin{array}{l}\widehat A = \widehat {A'},\,\widehat B = \widehat {B'},\widehat C = \widehat {C'}\\\dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{CA}}{{C'A'}}\end{array} \right.\)
Nên A sai.
Đáp án A.
Câu 2: Hãy lựa chọn câu đúng. Nếu tam giác $ABC$ đồng dạng với tam giác $MNP$ theo tỉ số \(k\) thì tam giác $MNP$ đồng dạng với tam giác $ABC$ bám theo tỉ số:
A. \(\dfrac{1}{{{k^2}}}\).
B. \(\dfrac{1}{{{k}}}\).
C. \({k^2}\).
D. \(k\).
Lời giải
Vì \(\Delta ABC\backsim\Delta MNP\) bám theo tỉ số \(k\) nên \(\dfrac{{AB}}{{MN}} = k \Rightarrow \dfrac{{MN}}{{AB}} = \dfrac{1}{k}\) .
Nên \(\Delta MNP\backsim\Delta ABC\) bám theo tỉ số \(\dfrac{{MN}}{{AB}} = \dfrac{1}{k}\) .
Đáp án B.
Câu 3: Hãy lựa chọn câu sai.
A. Hai tam giác đều nhau thì đồng dạng.
B. Hai tam giác đều luôn luôn đồng dạng cùng nhau.
C. Hai tam giác đồng dạng là nhị tam giác với toàn bộ những cặp góc ứng đều nhau và những cặp cạnh ứng tỉ lệ thành phần.
D. Hai tam giác vuông luôn luôn đồng dạng cùng nhau.
Lời giải
+ Hai tam giác đều nhau với những cặp góc ứng bằng nhau và những cạnh ứng đều nhau nên bọn chúng đồng dạng bám theo tỉ số \(1\) .
+ Hai tam giác đều sở hữu những góc đều vày \(60^\circ \) và những cạnh ứng tỉ lệ thành phần nên bọn chúng đồng dạng.
+ Hai tam giác vuông ko dĩ nhiên đồng dạng nên D sai.
Đáp án D.
Câu 4: Hãy lựa chọn câu vấn đáp chính. Nếu tam giác $ABC$ đồng dạng với tam giác \(A'B'C'\) bám theo tỉ số $k$ thì tỉ số chu vi của nhị tam giác cơ bằng
A. 1
B. \(\dfrac{1}{k}\).
C. \(k\).
D. \({k^2}\).
Lời giải
Vì tam giác \(ABC\) đồng dạng với tam giác \(A'B'C'\) bám theo tỉ số \(k\) nên \(\dfrac{{AB}}{{A'B'}} = \dfrac{{AC}}{{A'C'}} = \dfrac{{BC}}{{B'C'}} = k\) .
Ta với \(\dfrac{{AB}}{{A'B'}} = \dfrac{{AC}}{{A'C'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{AB + AC + BC}}{{A'B' + A'C' + B'C'}} = \dfrac{{{P_{ABC}}}}{{{P_{A'B'C'}}}} = k\).
Vậy tỉ số chu vi của nhị tam giác là \(k\) .
Đáp án C.
Câu 5: Hãy lựa chọn câu chính. Hai \({\rm{\Delta }}ABC\) và \({\rm{\Delta }}DEF\) với \(\widehat A = {80^0},\widehat B = {70^0},\)\(\widehat F = {30^0};\,BC = 6\,cm.\) Nếu \({\rm{\Delta }}ABC\) đồng dạng với \({\rm{\Delta }}DEF\) thì:
A. \(\widehat D = {170^0};\,EF = 6\,cm\).
B. \(\widehat E = {80^0};\,ED = 6\,cm\).
C. \(\widehat D = {70^0}\).
D. \(\widehat C = {30^0}\).
Lời giải
Vì tam giác \(ABC\) đồng dạng với tam giác $DEF$ nên
\(\widehat A = \widehat D = 80^\circ ;\,\widehat B = \widehat E = 70^\circ ;\,\\\widehat C = \widehat F = 30^\circ \)
Vậy \(\widehat C = {30^0}\) là chính.
Đáp án D.
Câu 6: Hình thang ABCD (AB // CD) với AB = 10cm, CD = 25cm, hai tuyến phố chéo cánh hạn chế nhau bên trên O.
Chọn xác minh đúng.
A. \(\Delta AOB\)\(\backsim\)\(\Delta COD\) với tỉ số đồng dạng \(k = 2\) .
B. \(\dfrac{{AO}}{{OC}} = \dfrac{2}{3}\)
C. \(\Delta AOB\)\(\backsim\)\(\Delta COD\) với tỉ số đồng dạng \(k = \dfrac{2}{5}\).
D. \(\Delta AOB\)\(\backsim\)\(\Delta COD\) với tỉ số đồng dạng \(k = \dfrac{5}{2}\).
Lời giải
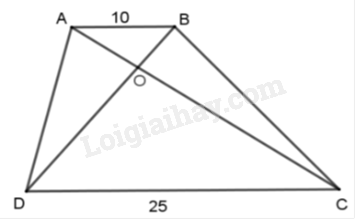
\(AB{\rm{//}}CD\) nên \(\Delta AOB\)\(\backsim\)\(\Delta COD.\) Tỉ số đồng dạng \(\dfrac{{AO}}{{OC}} = \dfrac{{BO}}{{OD}} = \dfrac{{AB}}{{CD}} = \dfrac{{10}}{{25}} = \dfrac{2}{5}.\)
Đáp án C.
Câu 7: Cho tam giác $ABC$ , điểm $M$ nằm trong cạnh $BC$ sao cho tới \(\dfrac{{MB}}{{MC}} = \dfrac{1}{2}.\) Đường trực tiếp trải qua M và tuy vậy song với $AC$ hạn chế $AB$ ở $D$ . Đường trực tiếp trải qua $M$ và tuy vậy song với $AB$ hạn chế $AC$ ở $E$ . hiểu chu vi tam giác $ABC$ vày \(30\,cm\) . Chu vi của những tam giác $DBM$ và $EMC$ theo lần lượt là
A. \(10\,cm;\,15\,cm\).
B. \(12\,cm;\,16\,cm\).
C. \(20\,cm;\,10\,cm\).
D. \(10\,cm;\,20\,cm\).
Lời giải
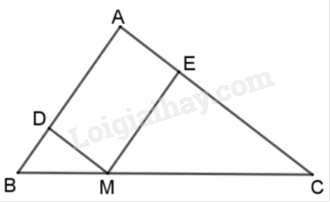
Ta với $MD$ // $AC$ nên \(\Delta DBM\)\(\backsim\)\(\Delta ABC\). Suy ra
\(\dfrac{{DB}}{{AB}} = \dfrac{{BM}}{{BC}} = \dfrac{{DM}}{{AC}} = \dfrac{{DB + BM + DM}}{{AB + BC + AC}}\)
Do cơ \(\dfrac{1}{3} = \dfrac{{{P_{\Delta BDM}}}}{{{P_{\Delta ABC}}}}.\)
Chu vi \(\Delta DBM\) vày \(30 \cdot \dfrac{1}{3} = 10\,\left( {cm} \right).\)
Ta với $ME$ // $AB$ nên \(\Delta EMC\)\(\backsim\)\(\Delta ABC.\) Suy ra
\(\dfrac{{EM}}{{AB}} = \dfrac{{MC}}{{BC}} = \dfrac{{EC}}{{AC}} = \dfrac{{EM + MC + EC}}{{AB + BC + AC}},\) vì thế \(\dfrac{2}{3} = \dfrac{{{P_{\Delta {\rm E}{\rm M}C}}}}{{{P_{\Delta ABC}}}}.\)
Chu vi \(\Delta EMC\) vày \(30 \cdot \dfrac{2}{3} = 20\,\left( {cm} \right).\)
Vậy chu vi \(\Delta DBM\) và chu vi \(\Delta EMC\) theo lần lượt là \(10\,cm;\,20\,cm\) .
Đáp án D.
Câu 8: Cho hình bình hành $ABCD$ . Trên lối chéo cánh $AC$ lấy điểm $E$ sao cho tới $AC = 3AE$ . Qua $E$ vẽ đường thẳng liền mạch tuy vậy song với $CD$ , hạn chế $AD$ và $BC$ bám theo trật tự ở $M$ và $N$ . Cho những xác minh sau:
(I) \(\Delta AME\)\(\backsim\)\(\Delta ADC,\) tỉ số đồng dạng \( k{ _1} = \dfrac{1}{3}.\)
(II) \(\Delta CBA\)\(\backsim\)\(\Delta ADC,\) tỉ số đồng dạng vày \({k_2} = 1\) .
(III) \(\Delta CNE\)\(\backsim\)\(\Delta ADC,\) tỉ số đồng dạng \({k_3} = \dfrac{2}{3}.\)
Chọn câu đúng.
A. (I) chính, (II) và (III) sai.
B. (I) và (II) chính, (III) sai.
C. Cả (I), (II), (III) đều chính.
D. Cả (I), (II), (III) đều sai.
Lời giải
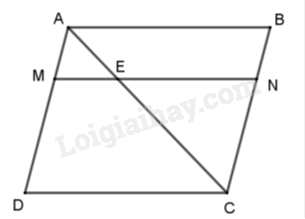
Vì \(ABCD\) là hình bình hành nên $ME$ // $DC$ và $EN$ // $AB$.
+ $ME$ // $DC$ nên \(\Delta AME\)\(\backsim\)\(\Delta ADC,\) tỉ số đồng dạng \(\dfrac{{AE}}{{AC}} = \dfrac{1}{3}.\)
+ Vì \(ABCD\) là hình bình hành nên \(\widehat B = \widehat D;\,AD = BC;\,AB = DC \)\(\Rightarrow \) \(\Delta CBA = \Delta ADC\) nên
\(\Delta CBA\)\(\backsim\)\(\Delta ADC,\) tỉ số đồng dạng vày $1$ .
+ $EN$ // $AB$ nên \(\Delta CNE\)\(\backsim\)\(\Delta CBA,\)do cơ \(\Delta CNE\)\(\backsim\)\(\Delta ADC,\) tỉ số đồng dạng \(\dfrac{{CE}}{{AC}} = \dfrac{2}{3}.\)
Vậy cả (I), (II), (III) đều chính.
Đáp án C.
